$$ % ASYMPTOTIC NOTATIONS \newcommand{\BigO}{\mathcal{O}} % NUMBER SYSTEMS \newcommand{\A}{\mathbb{A}} \newcommand{\B}{\mathbb{B}} \newcommand{\C}{\mathbb{C}} \newcommand{\D}{\mathbb{D}} \newcommand{\E}{\mathbb{E}} \newcommand{\F}{\mathbb{F}} \newcommand{\G}{\mathbb{G}} %\newcommand{\bbH}{\mathbb{H}} \newcommand{\I}{\mathbb{I}} \newcommand{\J}{\mathbb{J}} \newcommand{\K}{\mathbb{K}} %\newcommand{\bbL}{\mathbb{L}} \newcommand{\M}{\mathbb{M}} \newcommand{\N}{\mathbb{N}} %\newcommand{\bbO}{\mathbb{O}} %\newcommand{\bbP}{\mathbb{P}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\R}{\mathbb{R}} %\newcommand{\bbS}{\mathbb{S}} %\newcommand{\bbT}{\mathbb{T}} \newcommand{\U}{\mathbb{U}} \newcommand{\V}{\mathbb{V}} \newcommand{\W}{\mathbb{W}} \newcommand{\X}{\mathbb{X}} \newcommand{\Y}{\mathbb{Y}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\bbA}{\mathbb{A}} \newcommand{\bbB}{\mathbb{B}} \newcommand{\bbC}{\mathbb{C}} \newcommand{\bbD}{\mathbb{D}} \newcommand{\bbE}{\mathbb{E}} \newcommand{\bbF}{\mathbb{F}} \newcommand{\bbG}{\mathbb{G}} \newcommand{\bbH}{\mathbb{H}} \newcommand{\bbI}{\mathbb{I}} \newcommand{\bbJ}{\mathbb{J}} \newcommand{\bbK}{\mathbb{K}} \newcommand{\bbL}{\mathbb{L}} \newcommand{\bbM}{\mathbb{M}} \newcommand{\bbN}{\mathbb{N}} \newcommand{\bbO}{\mathbb{O}} \newcommand{\bbP}{\mathbb{P}} \newcommand{\bbQ}{\mathbb{Q}} \newcommand{\bbR}{\mathbb{R}} \newcommand{\bbS}{\mathbb{S}} \newcommand{\bbT}{\mathbb{T}} \newcommand{\bbU}{\mathbb{U}} \newcommand{\bbV}{\mathbb{V}} \newcommand{\bbW}{\mathbb{W}} \newcommand{\bbX}{\mathbb{X}} \newcommand{\bbY}{\mathbb{Y}} \newcommand{\bbZ}{\mathbb{Z}} % CALLICGRAPHIC SHORTCUTS \newcommand{\cA}{\mathcal{A}} \newcommand{\cB}{\mathcal{B}} \newcommand{\cC}{\mathcal{C}} \newcommand{\cD}{\mathcal{D}} \newcommand{\cE}{\mathcal{E}} \newcommand{\cF}{\mathcal{F}} \newcommand{\cG}{\mathcal{G}} \newcommand{\cH}{\mathcal{H}} \newcommand{\cI}{\mathcal{I}} \newcommand{\cJ}{\mathcal{J}} \newcommand{\cK}{\mathcal{K}} \newcommand{\cL}{\mathcal{L}} \newcommand{\cM}{\mathcal{M}} \newcommand{\cN}{\mathcal{N}} \newcommand{\cO}{\mathcal{O}} \newcommand{\cP}{\mathcal{P}} \newcommand{\cQ}{\mathcal{Q}} \newcommand{\cR}{\mathcal{R}} \newcommand{\cS}{\mathcal{S}} \newcommand{\cT}{\mathcal{T}} \newcommand{\cU}{\mathcal{U}} \newcommand{\cV}{\mathcal{V}} \newcommand{\cW}{\mathcal{W}} \newcommand{\cX}{\mathcal{X}} \newcommand{\cY}{\mathcal{Y}} \newcommand{\cZ}{\mathcal{Z}} % BRACES \newcommand{\set}[1]{\left\{ #1 \right\}} \newcommand{\dset}[2]{\left\{ #1 \ \middle| \ #2 \right\}} \newcommand{\alg}[1]{\left\langle #1 \right\rangle} \newcommand{\card}[1]{\left\lvert #1 \right\rvert} \newcommand{\length}[1]{\left\lvert #1 \right\rvert} \newcommand{\abs}[1]{\left\lvert #1 \right\rvert} \renewcommand{\mag}[1]{\left\lvert #1 \right\rvert} \newcommand{\norm}[1]{\left\lVert #1 \right\rVert} \newcommand{\scprod}[1]{\left\langle #1 \right\rangle} \newcommand{\ceil}[1]{\left\lceil #1 \right\rceil} \newcommand{\floor}[1]{\left\lfloor #1 \right\rfloor} \newcommand{\linsys}[2]{\left[\ #1 \ \middle| \ #2 \ \right]} \newcommand{\Sim}[1]{\text{Sim}\left( #1 \right)} \newcommand{\Tr}[1]{\mathsf{Tr}\left( #1 \right)} \newcommand{\bra}[1]{\left\langle #1 \right\rvert} \newcommand{\ket}[1]{\left\lvert #1 \right\rangle} \newcommand{\bracket}[2]{\left\langle #1 \ \middle| \ #2 \right\rangle} % BRACES SMALL (no adjusting) \newcommand{\sset}[1]{\{ #1 \}} \newcommand{\sdset}[2]{\{ #1 \ | \ #2 \}} \newcommand{\salg}[1]{\langle #1 \rangle} \newcommand{\scard}[1]{\lvert #1 \rvert} \newcommand{\slength}[1]{\lvert #1 \rvert} \newcommand{\sabs}[1]{\lvert #1 \rvert} \newcommand{\smag}[1]{\lvert #1 \rvert} \newcommand{\snorm}[1]{\lVert #1 \rVert} \newcommand{\sscprod}[1]{\langle #1 \rangle} \newcommand{\sceil}[1]{\lceil #1 \rceil} \newcommand{\sfloor}[1]{\lfloor #1 \rfloor} \newcommand{\slinsys}[2]{[\ #1 \ | \ #2 \ ]} \newcommand{\sSim}[1]{\text{Sim}( #1 )} \newcommand{\sTr}[1]{\mathsf{Tr}( #1 )} \newcommand{\sbra}[1]{\langle #1 \rvert} \newcommand{\sket}[1]{\lvert #1 \rangle} \newcommand{\sbracket}[2]{\langle #1 \ | \ #2 \rangle} % OPERATORS \newcommand{\conv}{*} \newcommand{\proj}{\text{proj}} % EMPTY SET \let\oldemptyset\emptyset \let\emptyset\varnothing % NOT IN SHORTCUT \newcommand{\nin}{\not\in} % CUSTOM STATISTICS AND PROBABILITY \newcommand{\Prob}[2][]{P_{#1}\left( #2 \right)} \newcommand{\cProb}[3][]{P_{#1}\left( #2 \,\middle|\, #3 \right)} \newcommand{\Dist}[2]{#1\left( #2 \right)} \newcommand{\cDist}[3]{#1\left( #2 \,\middle|\, #3 \right)} \newcommand{\hProb}[2][]{\hat{P}_{#1}\left( #2 \right)} \newcommand{\chProb}[2]{\hat{P}\left( #1 \,\middle|\, #2 \right)} \newcommand{\Var}[2][]{\operatorname{Var}_{#1}\left[ #2 \right]} \newcommand{\sd}[1]{\operatorname{sd}\left( #1 \right)} \newcommand{\Exp}[2][]{\mathbb{E}_{#1}\left[ #2 \right]} \newcommand{\cExp}[3][]{\mathbb{E}_{#1}\left[ #2 \,\middle|\, #3 \right]} \newcommand{\hExp}[2][]{\mathbb{\hat{E}_{#1}}\left[ #2 \right]} \newcommand{\chExp}[3][]{\mathbb{\hat{E}}_{#1}\left[ #2 \,\middle|\, #3 \right]} \newcommand{\Corr}[1]{\operatorname{Corr}\left[ #1 \right]} \newcommand{\Cov}[1]{\operatorname{Cov}\left(#1 \right)} \newcommand{\MSE}[2][]{\operatorname{MSE}_{#1}\left[ #2 \right]} \newcommand{\riid}{\stackrel{\text{i.i.d.}}{\sim}} \newcommand{\approxsim}{\stackrel{\text{approx.}}{\sim}} \newcommand{\ind}[1]{\mathbb{1}_{\set{#1}}} \newcommand{\eqiid}{\stackrel{\text{\tiny i.i.d.}}{=}} \newcommand{\eqind}{\stackrel{\text{\tiny ind.}}{=}} % BAYESIAN NETWORKS \newcommand{\indep}{\perp} \newcommand{\given}{\,\,|\,\,} \newcommand{\Pa}{\mathbf{Pa}} \newcommand{\dsep}[2]{\operatorname{d-sep}\left( #1 \,\middle|\, #2 \right)} % RANDOM VARIABLES \newcommand{\rA}{A} \newcommand{\rB}{B} \newcommand{\rC}{C} \newcommand{\rD}{D} \newcommand{\rE}{E} \newcommand{\rF}{F} \newcommand{\rG}{G} \newcommand{\rH}{H} \newcommand{\rI}{I} \newcommand{\rJ}{J} \newcommand{\rK}{K} \newcommand{\rL}{L} \newcommand{\rM}{M} \newcommand{\rN}{N} \newcommand{\rO}{O} \newcommand{\rP}{P} \newcommand{\rQ}{Q} \newcommand{\rR}{R} \newcommand{\rS}{S} \newcommand{\rT}{T} \newcommand{\rU}{U} \newcommand{\rV}{V} \newcommand{\rW}{W} \newcommand{\rX}{X} \newcommand{\rY}{Y} \newcommand{\rZ}{Z} % RANDOM VECTORS % declares a custom italic bold alphabet for random vectors \DeclareMathAlphabet{\mathbfit}{OML}{cmm}{b}{it} \newcommand{\rvA}{\mathbfit{A}} \newcommand{\rvB}{\mathbfit{B}} \newcommand{\rvC}{\mathbfit{C}} \newcommand{\rvD}{\mathbfit{D}} \newcommand{\rvE}{\mathbfit{E}} \newcommand{\rvF}{\mathbfit{F}} \newcommand{\rvG}{\mathbfit{G}} \newcommand{\rvH}{\mathbfit{H}} \newcommand{\rvI}{\mathbfit{I}} \newcommand{\rvJ}{\mathbfit{J}} \newcommand{\rvK}{\mathbfit{K}} \newcommand{\rvL}{\mathbfit{L}} \newcommand{\rvM}{\mathbfit{M}} \newcommand{\rvN}{\mathbfit{N}} \newcommand{\rvO}{\mathbfit{O}} \newcommand{\rvP}{\mathbfit{P}} \newcommand{\rvQ}{\mathbfit{Q}} \newcommand{\rvR}{\mathbfit{R}} \newcommand{\rvS}{\mathbfit{S}} \newcommand{\rvT}{\mathbfit{T}} \newcommand{\rvU}{\mathbfit{U}} \newcommand{\rvV}{\mathbfit{V}} \newcommand{\rvW}{\mathbfit{W}} \newcommand{\rvX}{\mathbfit{X}} \newcommand{\rvY}{\mathbfit{Y}} \newcommand{\rvZ}{\mathbfit{Z}} % MACHINE LEARNING \newcommand{\Risk}[1]{R\left(#1\right)} \newcommand{\empRisk}[1]{\widehat{R}\left(#1\right)} % RECOMMENDER SYSTEMS \newcommand{\RHR}[1]{\text{HR@}#1} \newcommand{\RDCG}[1]{\text{DCG@}#1} \newcommand{\RNDCG}[1]{\text{NDCG@}#1} \newcommand{\RHM}[1]{\text{HM@}#1} % ACCENTS % TODO: fix this, make spacing nice \newcommand{\Hm}{\mathsf{H}} \newcommand{\T}{\mathsf{T}} \newcommand{\Rev}{\mathsf{R}} \newcommand{\conj}[1]{\overline{ #1 }} % CUSTOM ALPHABETS \renewcommand{\S}{\Sigma} \newcommand{\Ss}{\Sigma^*} \newcommand{\Sp}{\Sigma^+} \newcommand{\Sbool}{\Sigma_{\text{bool}}} \newcommand{\Ssbool}{(\Sigma_{\text{bool}})^*} \newcommand{\Slogic}{\Sigma_{\text{logic}}} \newcommand{\Sslogic}{(\Sigma_{\text{logic}})^*} \newcommand{\Slat}{\Sigma_{\text{lat}}} \newcommand{\Sslat}{(\Sigma_{\text{lat}})^*} \newcommand{\Stastatur}{\Sigma_{\text{Tastatur}}} \newcommand{\Sstastatur}{(\Sigma_{\text{Tastatur}})^*} \newcommand{\Sm}{\Sigma_{m}} \newcommand{\Ssm}{\Sigma_{m}^*} \newcommand{\ZO}{\{0,1\}} \newcommand{\ZOs}{\{0,1\}^*} \newcommand{\hdelta}{\hat\delta} % OPERATORS % TODO: Should I design these as braces? \DeclareMathOperator{\id}{\text{id}} \DeclareMathOperator{\Kon}{\text{Kon}} \DeclareMathOperator{\cost}{\text{cost}} \DeclareMathOperator{\goal}{\text{goal}} \DeclareMathOperator{\Opt}{\text{Opt}} \DeclareMathOperator{\Bin}{\text{Bin}} \DeclareMathOperator{\Nummer}{\text{Nummer}} \DeclareMathOperator{\Prim}{\text{Prim}} \DeclareMathOperator{\Kl}{\text{Kl}} \DeclareMathOperator{\lcm}{lcm} \DeclareMathOperator{\glb}{glb} \DeclareMathOperator{\lub}{lub} \DeclareMathOperator{\im}{im} \DeclareMathOperator{\ord}{ord} \DeclareMathOperator{\rank}{rank} \DeclareMathOperator{\spn}{span} \DeclareMathOperator{\Cost}{Cost} \DeclareMathOperator{\order}{order} \DeclareMathOperator{\dist}{dist} \DeclareMathOperator{\cond}{cond} \DeclareMathOperator{\nnz}{nnz} \DeclareMathOperator{\sign}{sign} \DeclareMathOperator{\Count}{Count} \DeclareMathOperator{\Spur}{Spur} \DeclareMathOperator{\triu}{triu} \DeclareMathOperator{\cumsum}{cumsum} \DeclareMathOperator{\vectorize}{vectorize} \DeclareMathOperator{\matrixfy}{matrixfy} \DeclareMathOperator{\circul}{circul} \DeclareMathOperator{\dft}{dft} \DeclareMathOperator{\invdft}{invdft} \DeclareMathOperator{\ones}{ones} \DeclareMathOperator{\arcsinh}{arcsinh} \DeclareMathOperator{\arccosh}{arccosh} \DeclareMathOperator{\arctanh}{arctanh} \let\division\div \renewcommand\div{\operatorname{div}} \DeclareMathOperator{\rot}{rot} \DeclareMathOperator{\cis}{cis} \DeclareMathOperator{\grad}{grad} \DeclareMathOperator{\Hess}{Hess} \newcommand{\laplace}{\Delta} \DeclareMathOperator*{\argmin}{arg\,min} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator{\odd}{odd} \DeclareMathOperator{\even}{even} \DeclareMathOperator{\Proj}{Proj} \DeclareMathOperator{\softmax}{\text{softmax}} \DeclareMathOperator{\ReLU}{\text{ReLU}} \DeclareMathOperator{\pmi}{\text{pmi}} % TODO: fix these operator braces % TODO: think about which ones should have braces % and which one shouldn't. E.g., a function might need derivatives ' % or it might be used without argument, just in compositions \circ \newcommand{\diag}{\text{diag}} % CRYPTOGRAPHY \DeclareMathOperator{\concat}{ || } \DeclareMathOperator{\Enc}{Enc} \DeclareMathOperator{\Dec}{Dec} \DeclareMathOperator{\Gen}{Gen} \DeclareMathOperator{\Tag}{Tag} \DeclareMathOperator{\Vrfy}{Vrfy} \DeclareMathOperator{\MAC}{\text{MAC}} \newcommand{\AdvPRG}[2][]{\text{Adv}_{\text{PRG}}\left[ #2 \right]} \newcommand{\yes}{\text{yes}} \newcommand{\no}{\text{no}} \newcommand{\forallPPTTM}{\underset{\mathclap{\substack{\text{\tiny prob. poly-}\\\text{\tiny time TM}}}}{\forall}} \newcommand{\forallPTAdv}{\underset{\mathclap{\substack{\text{\tiny poly-time}\\\text{\tiny Adversaries}}}}{\forall}} % OPERATORS (OVERRIDDEN) \renewcommand\Re{\operatorname{Re}} \renewcommand\Im{\operatorname{Im}} % RELATIONS \newcommand{\mbeq}{\stackrel{!}{=}} \newcommand{\xor}{\mathrel{\text{xor}}} \newcommand{\relid}{\mathrel{\id}} \newcommand{\relrho}{\mathrel{\rho}} \newcommand{\relsigma}{\mathrel{\sigma}} \newcommand{\reltheta}{\mathrel{\theta}} \newcommand{\relsim}{\mathrel{\sim}} \newcommand{\relf}{\mathrel{f}} % RELATIONS (INVERSES) \newcommand{\invrelid}{\mathrel{\widehat{\id}}} \newcommand{\invrelrho}{\mathrel{\widehat{\rho}}} \newcommand{\invrelsigma}{\mathrel{\widehat{\sigma}}} \newcommand{\invreltheta}{\mathrel{\widehat{\theta}}} \newcommand{\invrelsim}{\mathrel{\widehat{\sim}}} \newcommand{\invrelf}{\mathrel{\widehat{f}}} % LINEAR TEMPORAL LOGIC (LTL) \newcommand{\until}{\texttt{\,\hstretch{0.7}{\boldsymbol{\cup}}\,}} \newcommand{\next}{\Circle} \newcommand{\eventually}{\Diamond} \newcommand{\always}{\square} % GLOBAL MATRICES AND VECTOR SETTINGS \newcommand{\boldm}[1] {\mathversion{bold}#1\mathversion{normal}} \newcommand{\mat}[1]{\mathbf{#1}} \renewcommand{\vec}[1]{\mathbf{#1}} % VECTORS (LATIN) \newcommand{\va}{\vec{a}} \newcommand{\vb}{\vec{b}} \newcommand{\vc}{\vec{c}} \newcommand{\vd}{\vec{d}} \newcommand{\ve}{\vec{e}} \newcommand{\vf}{\vec{f}} \newcommand{\vg}{\vec{g}} \newcommand{\vh}{\vec{h}} \newcommand{\vi}{\vec{i}} \newcommand{\vj}{\vec{j}} \newcommand{\vk}{\vec{k}} \newcommand{\vl}{\vec{l}} \newcommand{\vm}{\vec{m}} \newcommand{\vn}{\vec{n}} \newcommand{\vo}{\vec{o}} \newcommand{\vp}{\vec{p}} \newcommand{\vq}{\vec{q}} \newcommand{\vr}{\vec{r}} \newcommand{\vs}{\vec{s}} \newcommand{\vt}{\vec{t}} \newcommand{\vu}{\vec{u}} \newcommand{\vv}{\vec{v}} \newcommand{\vw}{\vec{w}} \newcommand{\vx}{\vec{x}} \newcommand{\vy}{\vec{y}} \newcommand{\vz}{\vec{z}} % VECTORS (LATIN) WITH TILDE ACCENT \newcommand{\vta}{\widetilde{\vec{a}}} \newcommand{\vtb}{\widetilde{\vec{b}}} \newcommand{\vtc}{\widetilde{\vec{c}}} \newcommand{\vtd}{\widetilde{\vec{d}}} \newcommand{\vte}{\widetilde{\vec{e}}} \newcommand{\vtf}{\widetilde{\vec{f}}} \newcommand{\vtg}{\widetilde{\vec{g}}} \newcommand{\vth}{\widetilde{\vec{h}}} \newcommand{\vti}{\widetilde{\vec{i}}} \newcommand{\vtj}{\widetilde{\vec{j}}} \newcommand{\vtk}{\widetilde{\vec{k}}} \newcommand{\vtl}{\widetilde{\vec{l}}} \newcommand{\vtm}{\widetilde{\vec{m}}} \newcommand{\vtn}{\widetilde{\vec{n}}} \newcommand{\vto}{\widetilde{\vec{o}}} \newcommand{\vtp}{\widetilde{\vec{p}}} \newcommand{\vtq}{\widetilde{\vec{q}}} \newcommand{\vtr}{\widetilde{\vec{r}}} \newcommand{\vts}{\widetilde{\vec{s}}} \newcommand{\vtt}{\widetilde{\vec{t}}} \newcommand{\vtu}{\widetilde{\vec{u}}} \newcommand{\vtv}{\widetilde{\vec{v}}} \newcommand{\vtw}{\widetilde{\vec{w}}} \newcommand{\vtx}{\widetilde{\vec{x}}} \newcommand{\vty}{\widetilde{\vec{y}}} \newcommand{\vtz}{\widetilde{\vec{z}}} % VECTORS (LATIN) WITH HAT ACCENT \newcommand{\vha}{\widehat{\vec{a}}} \newcommand{\vhb}{\widehat{\vec{b}}} \newcommand{\vhc}{\widehat{\vec{c}}} \newcommand{\vhd}{\widehat{\vec{d}}} \newcommand{\vhe}{\widehat{\vec{e}}} \newcommand{\vhf}{\widehat{\vec{f}}} \newcommand{\vhg}{\widehat{\vec{g}}} \newcommand{\vhh}{\widehat{\vec{h}}} \newcommand{\vhi}{\widehat{\vec{i}}} \newcommand{\vhj}{\widehat{\vec{j}}} \newcommand{\vhk}{\widehat{\vec{k}}} \newcommand{\vhl}{\widehat{\vec{l}}} \newcommand{\vhm}{\widehat{\vec{m}}} \newcommand{\vhn}{\widehat{\vec{n}}} \newcommand{\vho}{\widehat{\vec{o}}} \newcommand{\vhp}{\widehat{\vec{p}}} \newcommand{\vhq}{\widehat{\vec{q}}} \newcommand{\vhr}{\widehat{\vec{r}}} \newcommand{\vhs}{\widehat{\vec{s}}} \newcommand{\vht}{\widehat{\vec{t}}} \newcommand{\vhu}{\widehat{\vec{u}}} \newcommand{\vhv}{\widehat{\vec{v}}} \newcommand{\vhw}{\widehat{\vec{w}}} \newcommand{\vhx}{\widehat{\vec{x}}} \newcommand{\vhy}{\widehat{\vec{y}}} \newcommand{\vhz}{\widehat{\vec{z}}} % VECTORS (GREEK) \newcommand{\valpha}{\boldsymbol{\alpha}} \newcommand{\vbeta}{\boldsymbol{\beta}} \newcommand{\vgamma}{\boldsymbol{\gamma}} \newcommand{\vdelta}{\boldsymbol{\delta}} \newcommand{\vepsilon}{\boldsymbol{\epsilon}} \newcommand{\vvarepsilon}{\boldsymbol{\varepsilon}} \newcommand{\vzeta}{\boldsymbol{\zeta}} \newcommand{\veta}{\boldsymbol{\eta}} \newcommand{\vtheta}{\boldsymbol{\theta}} \newcommand{\viota}{\boldsymbol{\iota}} \newcommand{\vkappa}{\boldsymbol{\kappa}} \newcommand{\vlambda}{\boldsymbol{\lambda}} \newcommand{\vmu}{\boldsymbol{\mu}} \newcommand{\vnu}{\boldsymbol{\nu}} \newcommand{\vxi}{\boldsymbol{\xi}} % omikron is just latin 'o' \newcommand{\vpi}{\boldsymbol{\pi}} \newcommand{\vrho}{\boldsymbol{\rho}} \newcommand{\vsigma}{\boldsymbol{\sigma}} \newcommand{\vtau}{\boldsymbol{\tau}} \newcommand{\vupsilon}{\boldsymbol{\upsilon}} \newcommand{\vphi}{\boldsymbol{\phi}} \newcommand{\vvarphi}{\boldsymbol{\varphi}} \newcommand{\vchi}{\boldsymbol{\chi}} \newcommand{\vpsi}{\boldsymbol{\psi}} \newcommand{\vomega}{\boldsymbol{\omega}} % VECTORS (GREEK) WITH TILDE ACCENT \newcommand{\vtalpha}{\widetilde{\valpha}} \newcommand{\vtbeta}{\widetilde{\vbeta}} \newcommand{\vtgamma}{\widetilde{\vgamma}} \newcommand{\vtdelta}{\widetilde{\vdelta}} \newcommand{\vtepsilon}{\widetilde{\vepsilon}} \newcommand{\vtvarepsilon}{\widetilde{\vvarepsilon}} \newcommand{\vtzeta}{\widetilde{\vzeta}} \newcommand{\vteta}{\widetilde{\veta}} \newcommand{\vttheta}{\widetilde{\vtheta}} \newcommand{\vtiota}{\widetilde{\viota}} \newcommand{\vtkappa}{\widetilde{\vkappa}} \newcommand{\vtlambda}{\widetilde{\vlambda}} \newcommand{\vtmu}{\widetilde{\vmu}} \newcommand{\vtnu}{\widetilde{\vnu}} \newcommand{\vtxi}{\widetilde{\vxi}} % omikron is just latin 'o' \newcommand{\vtpi}{\widetilde{\vpi}} \newcommand{\vtrho}{\widetilde{\vrho}} \newcommand{\vtsigma}{\widetilde{\vsigma}} \newcommand{\vttau}{\widetilde{\vtau}} \newcommand{\vtupsilon}{\widetilde{\vupsilon}} \newcommand{\vtphi}{\widetilde{\vphi}} \newcommand{\vtvarphi}{\widetilde{\vvarphi}} \newcommand{\vtchi}{\widetilde{\vchi}} \newcommand{\vtpsi}{\widetilde{\vpsi}} \newcommand{\vtomega}{\widetilde{\vomega}} % VECTORS (GREEK) WITH HAT ACCENT \newcommand{\vhalpha}{\widehat{\valpha}} \newcommand{\vhbeta}{\widehat{\vbeta}} \newcommand{\vhgamma}{\widehat{\vgamma}} \newcommand{\vhdelta}{\widehat{\vdelta}} \newcommand{\vhepsilon}{\widehat{\vepsilon}} \newcommand{\vhvarepsilon}{\widehat{\vvarepsilon}} \newcommand{\vhzeta}{\widehat{\vzeta}} \newcommand{\vheta}{\widehat{\veta}} \newcommand{\vhtheta}{\widehat{\vtheta}} \newcommand{\vhiota}{\widehat{\viota}} \newcommand{\vhkappa}{\widehat{\vkappa}} \newcommand{\vhlambda}{\widehat{\vlambda}} \newcommand{\vhmu}{\widehat{\vmu}} \newcommand{\vhnu}{\widehat{\vnu}} \newcommand{\vhxi}{\widehat{\vxi}} % omikron is just latin 'o' \newcommand{\vhpi}{\widehat{\vpi}} \newcommand{\vhrho}{\widehat{\vrho}} \newcommand{\vhsigma}{\widehat{\vsigma}} \newcommand{\vhtau}{\widehat{\vthau}} \newcommand{\vhupsilon}{\widehat{\vupsilon}} \newcommand{\vhphi}{\widehat{\vphi}} \newcommand{\vhvarphi}{\widehat{\vvarphi}} \newcommand{\vhchi}{\widehat{\vchi}} \newcommand{\vhpsi}{\widehat{\vpsi}} \newcommand{\vhomega}{\widehat{\vomega}} % MATRICES (LATIN) \newcommand{\MA}{\mat{A}} \newcommand{\MB}{\mat{B}} \newcommand{\MC}{\mat{C}} \newcommand{\MD}{\mat{D}} \newcommand{\ME}{\mat{E}} \newcommand{\MF}{\mat{F}} \newcommand{\MG}{\mat{G}} \newcommand{\MH}{\mat{H}} \newcommand{\MI}{\mat{I}} \newcommand{\MJ}{\mat{J}} \newcommand{\MK}{\mat{K}} \newcommand{\ML}{\mat{L}} \newcommand{\MM}{\mat{M}} \newcommand{\MN}{\mat{N}} \newcommand{\MO}{\mat{0}} \newcommand{\MP}{\mat{P}} \newcommand{\MQ}{\mat{Q}} \newcommand{\MR}{\mat{R}} \newcommand{\MS}{\mat{S}} \newcommand{\MT}{\mat{T}} \newcommand{\MU}{\mat{U}} \newcommand{\MV}{\mat{V}} \newcommand{\MW}{\mat{W}} \newcommand{\MX}{\mat{X}} \newcommand{\MY}{\mat{Y}} \newcommand{\MZ}{\mat{Z}} % MATRICES (LATIN) TILDE \newcommand{\MtA}{\widetilde{\mat{A}}} \newcommand{\MtB}{\widetilde{\mat{B}}} \newcommand{\MtC}{\widetilde{\mat{C}}} \newcommand{\MtD}{\widetilde{\mat{D}}} \newcommand{\MtE}{\widetilde{\mat{E}}} \newcommand{\MtF}{\widetilde{\mat{F}}} \newcommand{\MtG}{\widetilde{\mat{G}}} \newcommand{\MtH}{\widetilde{\mat{H}}} \newcommand{\MtI}{\widetilde{\mat{I}}} \newcommand{\MtJ}{\widetilde{\mat{J}}} \newcommand{\MtK}{\widetilde{\mat{K}}} \newcommand{\MtL}{\widetilde{\mat{L}}} \newcommand{\MtM}{\widetilde{\mat{M}}} \newcommand{\MtN}{\widetilde{\mat{N}}} \newcommand{\MtO}{\widetilde{\mat{0}}} \newcommand{\MtP}{\widetilde{\mat{P}}} \newcommand{\MtQ}{\widetilde{\mat{Q}}} \newcommand{\MtR}{\widetilde{\mat{R}}} \newcommand{\MtS}{\widetilde{\mat{S}}} \newcommand{\MtT}{\widetilde{\mat{T}}} \newcommand{\MtU}{\widetilde{\mat{U}}} \newcommand{\MtV}{\widetilde{\mat{V}}} \newcommand{\MtW}{\widetilde{\mat{W}}} \newcommand{\MtX}{\widetilde{\mat{X}}} \newcommand{\MtY}{\widetilde{\mat{Y}}} \newcommand{\MtZ}{\widetilde{\mat{Z}}} % MATRICES (LATIN) HAT \newcommand{\MhA}{\widehat{\mat{A}}} \newcommand{\MhB}{\widehat{\mat{B}}} \newcommand{\MhC}{\widehat{\mat{C}}} \newcommand{\MhD}{\widehat{\mat{D}}} \newcommand{\MhE}{\widehat{\mat{E}}} \newcommand{\MhF}{\widehat{\mat{F}}} \newcommand{\MhG}{\widehat{\mat{G}}} \newcommand{\MhH}{\widehat{\mat{H}}} \newcommand{\MhI}{\widehat{\mat{I}}} \newcommand{\MhJ}{\widehat{\mat{J}}} \newcommand{\MhK}{\widehat{\mat{K}}} \newcommand{\MhL}{\widehat{\mat{L}}} \newcommand{\MhM}{\widehat{\mat{M}}} \newcommand{\MhN}{\widehat{\mat{N}}} \newcommand{\MhO}{\widehat{\mat{0}}} \newcommand{\MhP}{\widehat{\mat{P}}} \newcommand{\MhQ}{\widehat{\mat{Q}}} \newcommand{\MhR}{\widehat{\mat{R}}} \newcommand{\MhS}{\widehat{\mat{S}}} \newcommand{\MhT}{\widehat{\mat{T}}} \newcommand{\MhU}{\widehat{\mat{U}}} \newcommand{\MhV}{\widehat{\mat{V}}} \newcommand{\MhW}{\widehat{\mat{W}}} \newcommand{\MhX}{\widehat{\mat{X}}} \newcommand{\MhY}{\widehat{\mat{Y}}} \newcommand{\MhZ}{\widehat{\mat{Z}}} % MATRICES (GREEK) \newcommand{\MGamma}{\mat{\Gamma}} \newcommand{\MDelta}{\mat{\Delta}} \newcommand{\MTheta}{\mat{\Theta}} \newcommand{\MLambda}{\mat{\Lambda}} \newcommand{\MXi}{\mat{\Xi}} \newcommand{\MPi}{\mat{\Pi}} \newcommand{\MSigma}{\mat{\Sigma}} \newcommand{\MUpsilon}{\mat{\Upsilon}} \newcommand{\MPhi}{\mat{\Phi}} \newcommand{\MPsi}{\mat{\Psi}} \newcommand{\MOmega}{\mat{\Omega}} % MATRICES (GREEK) TILDE \newcommand{\MtGamma}{\widetilde{\MGamma}} \newcommand{\MtDelta}{\widetilde{\MDelta}} \newcommand{\MtTheta}{\widetilde{\MTheta}} \newcommand{\MtLambda}{\widetilde{\MLambda}} \newcommand{\MtXi}{\widetilde{\MXi}} \newcommand{\MtPi}{\widetilde{\MPi}} \newcommand{\MtSigma}{\widetilde{\MSigma}} \newcommand{\MtUpsilon}{\widetilde{\MUpsilon}} \newcommand{\MtPhi}{\widetilde{\MPhi}} \newcommand{\MtPsi}{\widetilde{\MPsi}} \newcommand{\MtOmega}{\widetilde{\MOmega}} % MATRICES (GREEK) HAT \newcommand{\MhGamma}{\widehat{\MGamma}} \newcommand{\MhDelta}{\widehat{\MDelta}} \newcommand{\MhTheta}{\widehat{\MTheta}} \newcommand{\MhLambda}{\widehat{\MLambda}} \newcommand{\MhXi}{\widehat{\MXi}} \newcommand{\MhPi}{\widehat{\MPi}} \newcommand{\MhSigma}{\widehat{\MSigma}} \newcommand{\MhUpsilon}{\widehat{\MUpsilon}} \newcommand{\MhPhi}{\widehat{\MPhi}} \newcommand{\MhPsi}{\widehat{\MPsi}} \newcommand{\MhOmega}{\widehat{\MOmega}} % TENSORS (LATIN) \DeclareMathAlphabet{\mathsfit}{\encodingdefault}{\sfdefault}{m}{sl} \SetMathAlphabet{\mathsfit}{bold}{\encodingdefault}{\sfdefault}{bx}{n} \newcommand{\tens}[1]{\bm{\mathsfit{#1}}} \newcommand{\TA}{\tens{A}} \newcommand{\TB}{\tens{B}} \newcommand{\TC}{\tens{C}} \newcommand{\TD}{\tens{D}} \newcommand{\TE}{\tens{E}} \newcommand{\TF}{\tens{F}} \newcommand{\TG}{\tens{G}} \renewcommand{\TH}{\tens{H}} \newcommand{\TI}{\tens{I}} \newcommand{\TJ}{\tens{J}} \newcommand{\TK}{\tens{K}} \newcommand{\TL}{\tens{L}} \newcommand{\TM}{\tens{M}} \newcommand{\TN}{\tens{N}} \newcommand{\TO}{\tens{O}} \newcommand{\TP}{\tens{P}} \newcommand{\TQ}{\tens{Q}} \newcommand{\TR}{\tens{R}} \newcommand{\TS}{\tens{S}} \newcommand{\TT}{\tens{T}} \newcommand{\TU}{\tens{U}} \newcommand{\TV}{\tens{V}} \newcommand{\TW}{\tens{W}} \newcommand{\TX}{\tens{X}} \newcommand{\TY}{\tens{Y}} \newcommand{\TZ}{\tens{Z}} % MATRIX SPACING BARS (for representing row/column-vectors) \newcommand{\vertbar}{\rule[-1ex]{0.5pt}{4ex}} \newcommand{\horzbar}{\rule[.5ex]{4ex}{0.5pt}} \newcommand{\svertbar}{\rule[-0.5ex]{0.5pt}{2ex}} \newcommand{\veclines}[1]{ \begin{matrix} \svertbar\\ \displaystyle #1\\ \svertbar\\ \end{matrix} } % CUSTOM NUMERICS \newcommand{\EPS}{\text{EPS}} \DeclareMathOperator{\rd}{rd} \newcommand{\op}{\mathbin{\text{op}}} \newcommand{\mop}{\mathbin{\widetilde{\text{op}}}} % CUSTOM CALCULUS \newcommand{\evalat}[2]{\left. #1 \right|_{#2}} \newcommand{\evalint}[3]{\left. #1 \right|_{#2}^{#3}} \newcommand{\fpartial}[2]{\frac{\partial #1}{\partial #2}} % TILDE CHARACTERS \newcommand{\wta}{\widetilde{a}} \newcommand{\wtb}{\widetilde{b}} \newcommand{\wtc}{\widetilde{c}} \newcommand{\wtd}{\widetilde{d}} \newcommand{\wte}{\widetilde{e}} \newcommand{\wtf}{\widetilde{f}} \newcommand{\wtg}{\widetilde{g}} \newcommand{\wth}{\widetilde{h}} \newcommand{\wti}{\widetilde{i}} \newcommand{\wtj}{\widetilde{j}} \newcommand{\wtk}{\widetilde{k}} \newcommand{\wtl}{\widetilde{l}} \newcommand{\wtm}{\widetilde{m}} \newcommand{\wtn}{\widetilde{n}} \newcommand{\wto}{\widetilde{o}} \newcommand{\wtp}{\widetilde{p}} \newcommand{\wtq}{\widetilde{q}} \newcommand{\wtr}{\widetilde{r}} \newcommand{\wts}{\widetilde{s}} \newcommand{\wtt}{\widetilde{t}} \newcommand{\wtu}{\widetilde{u}} \newcommand{\wtv}{\widetilde{v}} \newcommand{\wtw}{\widetilde{w}} \newcommand{\wtx}{\widetilde{x}} \newcommand{\wty}{\widetilde{y}} \newcommand{\wtz}{\widetilde{z}} \newcommand{\wtA}{\widetilde{A}} \newcommand{\wtB}{\widetilde{B}} \newcommand{\wtC}{\widetilde{C}} \newcommand{\wtD}{\widetilde{D}} \newcommand{\wtE}{\widetilde{E}} \newcommand{\wtF}{\widetilde{F}} \newcommand{\wtG}{\widetilde{G}} \newcommand{\wtH}{\widetilde{H}} \newcommand{\wtI}{\widetilde{I}} \newcommand{\wtJ}{\widetilde{J}} \newcommand{\wtK}{\widetilde{K}} \newcommand{\wtL}{\widetilde{L}} \newcommand{\wtM}{\widetilde{M}} \newcommand{\wtN}{\widetilde{N}} \newcommand{\wtO}{\widetilde{O}} \newcommand{\wtP}{\widetilde{P}} \newcommand{\wtQ}{\widetilde{Q}} \newcommand{\wtR}{\widetilde{R}} \newcommand{\wtS}{\widetilde{S}} \newcommand{\wtT}{\widetilde{T}} \newcommand{\wtU}{\widetilde{U}} \newcommand{\wtV}{\widetilde{V}} \newcommand{\wtW}{\widetilde{W}} \newcommand{\wtX}{\widetilde{X}} \newcommand{\wtY}{\widetilde{Y}} \newcommand{\wtZ}{\widetilde{Z}} % HAT CHARACTERS \newcommand{\wha}{\widehat{a}} \newcommand{\whb}{\widehat{b}} \newcommand{\whc}{\widehat{c}} \newcommand{\whd}{\widehat{d}} \newcommand{\whe}{\widehat{e}} \newcommand{\whf}{\widehat{f}} \newcommand{\whg}{\widehat{g}} \newcommand{\whh}{\widehat{h}} \newcommand{\whi}{\widehat{i}} \newcommand{\whj}{\widehat{j}} \newcommand{\whk}{\widehat{k}} \newcommand{\whl}{\widehat{l}} \newcommand{\whm}{\widehat{m}} \newcommand{\whn}{\widehat{n}} \newcommand{\who}{\widehat{o}} \newcommand{\whp}{\widehat{p}} \newcommand{\whq}{\widehat{q}} \newcommand{\whr}{\widehat{r}} \newcommand{\whs}{\widehat{s}} \newcommand{\wht}{\widehat{t}} \newcommand{\whu}{\widehat{u}} \newcommand{\whv}{\widehat{v}} \newcommand{\whw}{\widehat{w}} \newcommand{\whx}{\widehat{x}} \newcommand{\why}{\widehat{y}} \newcommand{\whz}{\widehat{z}} \newcommand{\whA}{\widehat{A}} \newcommand{\whB}{\widehat{B}} \newcommand{\whC}{\widehat{C}} \newcommand{\whD}{\widehat{D}} \newcommand{\whE}{\widehat{E}} \newcommand{\whF}{\widehat{F}} \newcommand{\whG}{\widehat{G}} \newcommand{\whH}{\widehat{H}} \newcommand{\whI}{\widehat{I}} \newcommand{\whJ}{\widehat{J}} \newcommand{\whK}{\widehat{K}} \newcommand{\whL}{\widehat{L}} \newcommand{\whM}{\widehat{M}} \newcommand{\whN}{\widehat{N}} \newcommand{\whO}{\widehat{O}} \newcommand{\whP}{\widehat{P}} \newcommand{\whQ}{\widehat{Q}} \newcommand{\whR}{\widehat{R}} \newcommand{\whS}{\widehat{S}} \newcommand{\whT}{\widehat{T}} \newcommand{\whU}{\widehat{U}} \newcommand{\whV}{\widehat{V}} \newcommand{\whW}{\widehat{W}} \newcommand{\whX}{\widehat{X}} \newcommand{\whY}{\widehat{Y}} \newcommand{\whZ}{\widehat{Z}} % ARGUMENT DOT \newcommand{\argdot}{\,\cdot\,} % QUANTUM MECHANICS \newcommand{\gates}[1]{\stackrel{#1}{\longrightarrow}} \newcommand{\sbell}{\ket{\psi_{\text{Bell}}}} % GYROSPACES \newcommand{\vzero}{\mathbf{0}} \newcommand{\gyr}{\operatorname{gyr}} % ABSTRACT ALGEBRA \newcommand{\Aut}{\operatorname{Aut}} $$
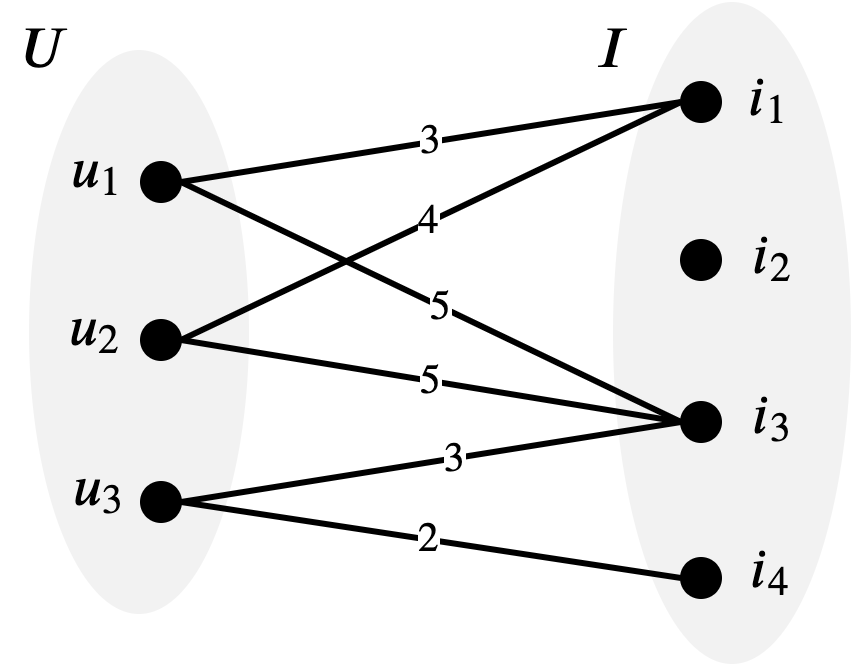
Recommender systems are at the heart of many of today's online platforms. Numerous approaches for collaborative filtering from implicit feedback data have been invented over the years. This blogpost provides an overview of several of these recommender algorithms.
Posted by Andreas Bloch under the assistance of Octavian Ganea and Gary Bécigneul on December 16, 2019
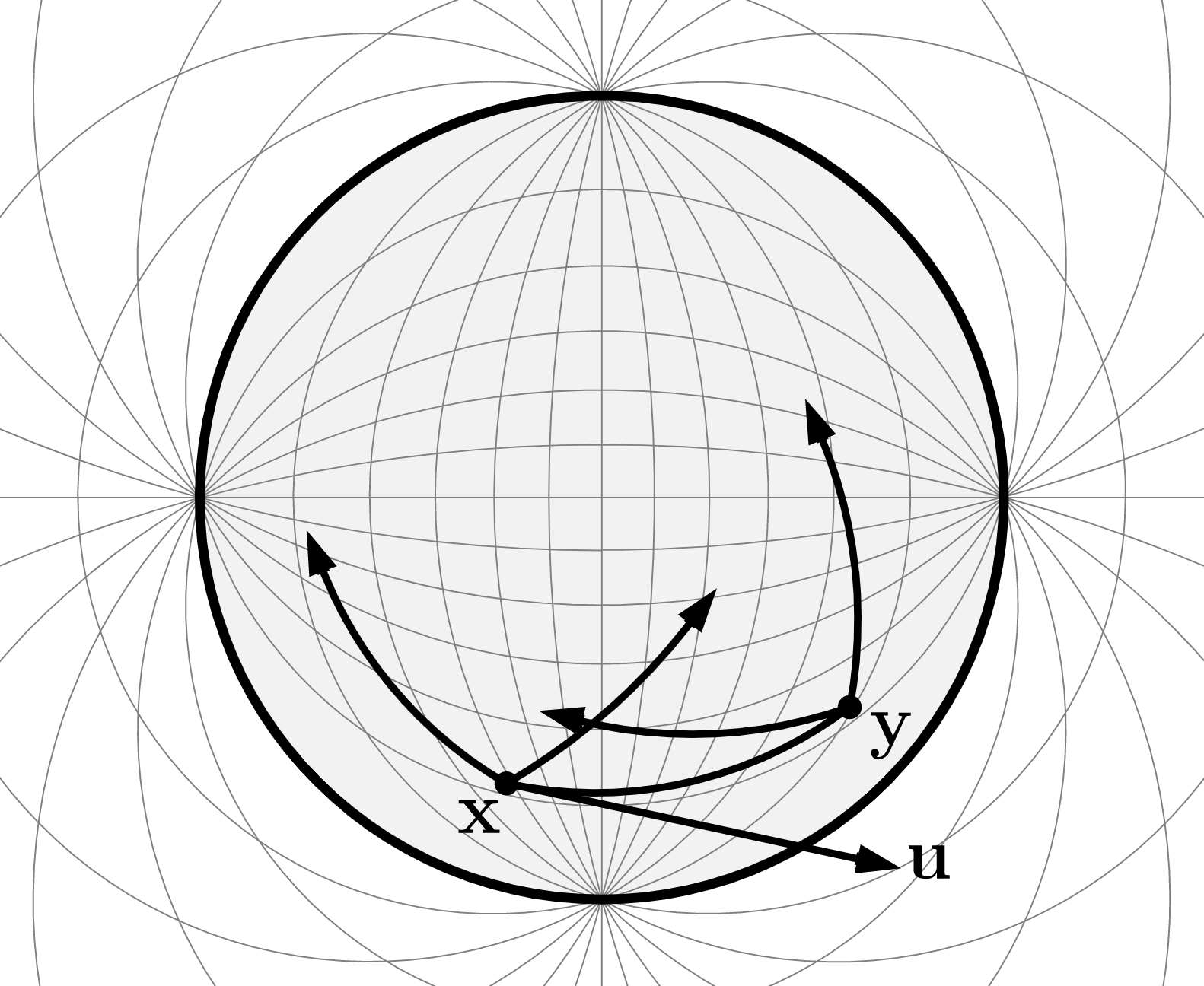
This blogpost presents a geometric model that harnesses the formalism gyrovector spaces in order to capture all three geometries of constant curvature at once. Furthermore, the presented model allows to smoothly interpolate between different curvatures in order to learn the curvature of spaces jointly with the embeddings.
Posted by Andreas Bloch in collaboration with Ondrej Skopek and Gregor Bachmann under the assistance of Octavian Ganea and Gary Bécigneul on November 21, 2019
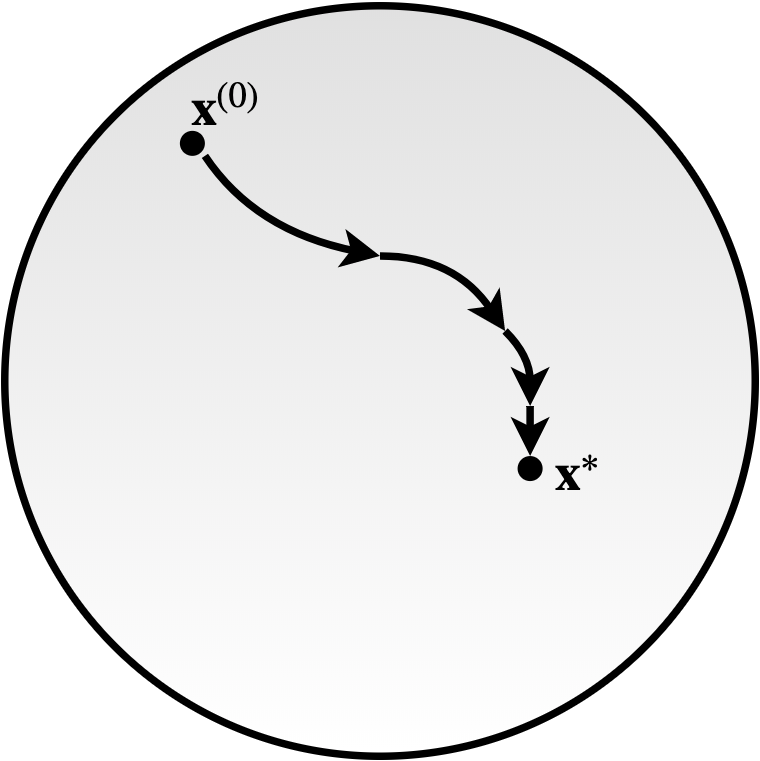
Stochastic Gradient Descent (SGD) is the default workhorse for most of today's machine learning algorithms. While the majority of SGD applications is concerned with Euclidean spaces, recent advances also explored the potential of Riemannian manifolds. This blogpost explains how the concept of SGD is generalized to Riemannian manifolds.
Posted by Andreas Bloch under the assistance of Octavian Ganea and Gary Bécigneul on October 15, 2019